COGS201 学习笔记 week 1
Representations 和 Procedures的区别
Representations: 你所知道的
Procedures: 你所在做的
Thinking = Representations + Procedures
Representations的例子
Concepts概念 (what is a “chair”? 什么是“椅子”?)
Facts事实 (Convocation Hall has a balcony 集会厅设有阳台)
Production Rules 规则 (IF the door has a knob, THEN I can turn the knob 如果…那么…)
Memories 记忆(读取) (how I felt when I woke up yesterday)
Sensations感受 (it’s cold in here)
Procedures 的例子
• Logical reasoning逻辑推理
• Solving a problem解决问题
• Making a plan制定计划
• Processing sensory information处理感官信息
• Moving your body身体动作
• Allocating attention分配注意力
• Speaking out loud大声说话
The Tri-Level Hypothesis 三层次分析
Computational (进化):系统正在解决信息处理问题是什么 - 系统的目标是?
• Play a chess game and beat your opponent.下棋并击败对手。
• What are the rules of chess? What moves can you make? How do
you win? 国际象棋的规则是什么?可以走哪些棋?如何获胜?
算法表征层面 Algorithmic/Representation (认知):实现这个目标需要哪些信息处理步骤和计算?
• How do you decide what move to make? How do you think “six
moves ahead” and judge what outcome is best?
如何决定下一步棋?如何预判“六步之后”并判断最佳结果?
• How do you represent the state of the chess board? The possible
outcomes?
如何描述棋盘状态?如何描述可能的结果?
• Do you need to represent every possible state, or can the states
be “narrowed down”?
是否需要描述所有可能状态,还是可以“缩小范围”?
物理实现层面 Implementation/Physical (神经科学):物理设备,例如生物体,实际上是如何执行这些信息处理步骤的?
•How does the computer work? How do its circuits carry out
instructions?
计算机如何运作?其电路如何执行指令?
•Do we need special hardware in order to make the chess playing
process more efficient?
我们是否需要特殊硬件来提高下棋过程的效率?
Mind vs Computer vs Brain
| Mind(心智) | Computer(计算机) | Brain(大脑) |
|---|---|---|
| Representations(表征) | Data Structures(数据结构) | Neuron Structure(神经结构) |
| Procedures(过程) | Algorithms(算法) | Firing Rules(放电规则) |
| Input(输入) | Keyboard, Mouse, etc(键盘、鼠标等) | Sensory Experience(感觉经验) |
| Output(输出) | Change to display or data(显示/数据变化) | Physical Actions(物理动作) |
Premises and conclusions 前提和结论
Premise 1: If it is raining, then you should take an umbrella.
Premise 2: It is raining now.
Conclusion: I should take an umbrella.
通用版本
Fact 1: If P is true, then R is true.
Fact 2: P is true.
Conclusion: R is true.
我们将fact(如“正在下雨”或“我需要一把伞”)表示为单个字母或命题。
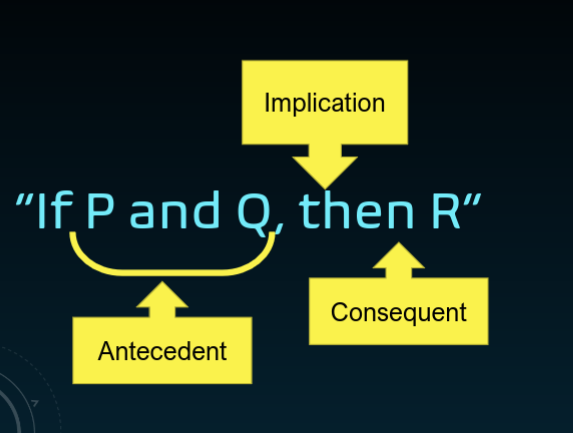
Implication(蕴含/条件句)
Antecedent(前件/条件部分):
Consequent(后件/结论部分)
LOGIC OPERATORS 逻辑运算符
P ˄ Q “P and Q.”
P ˅ Q “P or Q.”
¬ P “Not P.”
P → Q “If P, then Q.” (or “P implies Q”)
OR 和 XOR 区别
xor在or的基础上如果都相等则为false
DEDUCTIVE REASONING 演绎推理
在演绎推理中,若前提为真,且逻辑结构严谨,则结论必然为真。这被称为“有效”的三段论
两种类型
Modus Ponens 肯定前件式
Modus Tollens 否定后件式
Modus Ponens肯定前件式:
$$
Premise 1:P → Q \
Premise 2:P \
Conclusion:Q
$$
Premise 1: If you have $3, you can buy a coffee.
Premise 2: I have $3.
Conclusion: I can buy a coffee.
Modus Tollens 否定后件式
$$
Premise 1:P → Q \
Premise 2:¬Q \
Conclusion:¬P
$$
Premise 1: If this is a flowering plant, then it has seeds.
Premise 2: It has no seeds.
Conclusion: It is not a flowering plant.
VALIDITY AND truth
Valid but false
Premise 1: “If airplanes are birds, then I am 1000 years old.”
Premise 2: “Airplanes are birds.”
Conclusion: “I am 1000 years old.”
条件不可能发生
INVALID LOGIC
• Premise 1: If there is a hurricane, there will be winds of at least 74 mph.
• Premise 2: There are winds of at least 74 mph.
• Conclusion: There is a hurricane
风速超过74的原因很多
• Premise 1: P -> Q
• Premise 2: Q
• Conclusion: P
• 若P为真,则Q为真。
• 但若P不为真,Q可能为真也可能不为真;我们无法确定。
• 因此我们不能必然得出P为真的结论。
PREDICATE LOGIC 谓词逻辑
Predicate Logic符号
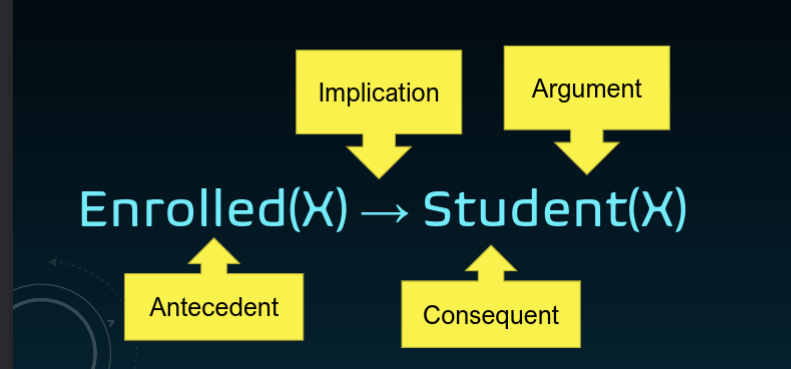
Antecedent(前件/条件):Enrolled(X)
Implication(蕴含/如果…那么…):→
Consequent(后件/结论):Student()
Argument(论元/参数): X
Generalizing Logic 逻辑泛化
“If Anne is enrolled, then Anne is a student.”
Proposition: P → Q
• (P = “Anne is enrolled”)
• (Q = “Anne is a student”)
“If Bob is enrolled, then Bob is a student.”
Proposition: R → S
• (R = “Bob is enrolled” = different from P!)
• (S = “Bob is a student” = different from Q!)
[!NOTE]
在命题逻辑里,P、Q、R、S 都是“整句命题”。
只要换了人名(Anne→Bob),就变成了新的命题字母,必须重新定义
If Anne is enrolled, then Anne is a student.”
Predicate: enrolled(anne) → student(anne)
enrolled(bob) → student(bob)
使用变量 X, 我们可以对该陈述进行编码:
enrolled(X) → student(X)
“For all entities X, if X is enrolled, then X is a student.”
谓词逻辑:
关系
例如:
parent(george,susan).
• “George is Susan’s parent”(顺序很重要!)
loves(marwa,math).
• “Marwa loves math”
Three Types of logical Reasoning 逻辑推理的三种类型
- Deductive
- Inductive
- Abductive
Deductive
1.Based on airtight rules of inference(基于严密的推理规则(airtight = 密不透风、不会出错))
比如:肯定前件(Modus Ponens)、三段论等。规则本身保证“从前提到结论”的形式是对的。
- **核心!!:**If the premises are true… conclusion MUST be true
这是演绎推理最重要的性质:必然性。
它强调两个条件都要满足:
a.premises(前提)是真的
b.推理过程是 valid(形式有效)⇒ 才能保证结论 must 为真。
3.Formal logic is deductive
形式逻辑(命题逻辑、谓词逻辑)主要研究的就是这种“保证必然正确”的推理形式:
不看内容像不像真实世界,只看“推理结构”是否有效
4.Prolog is deductive
[!CAUTION]
核心
只要前提是真的,并且推理规则用得“有效”(valid),结论就一定是真的。
Inductive
但Deducive无法解释我们如何获取事实。那我们如何知道前提premise是真实的?
1.归纳推理通过概括创造新知识。
2.观察大量实例。
3.若某些事实在所有已知实例中恒定存在,我们便可推断它们永远成立。
例如:
1.我们观察了1000只乌鸦。
2.它们全都长着黑色的羽毛。
3.因此,很可能所有乌鸦都长着黑色的羽毛。
证据越多,我们就能越确定但总有一天我们可能会发现一个反例……
Abductive
Premise 1:若我们的太空探测器坠毁,我们将与其失去联系。
Premise 2:我们已与该太空探测器失去联系。
Premise 3:该太空探测器可能已坠毁…(或可能发生了其他故障)
在知识库中搜索可能的原因->找出最可能或最简单的原因->奥卡姆剃刀原则(Occam’s razor)